Memoization: Enhancing Algorithmic Efficiency Through Caching

“It would be useful if computers could learn from experience and thus automatically improve the efficiency of their own programs during execution. A simple but effective rote-learning facility can be provided within the framework of a suitable programming language.” ~ Donald Michie

Since the beginning of time, humans have always tried to optimize their life. They discovered new ways of constructing buildings, creating roads to get faster from one point to another, or just developing their language for better communication.

In the world of algorithms, optimization is one of the golden keys that unlocks the doors to efficiency and precision. Since the beginning of computing, scientists and developers have always aimed to enhance performance, therefore many of them dedicated a large amount of their time trying to find optimality in every segment of this universe.

As technology advances at an unprecedented pace, the importance of performance in computing becomes more and more essential; even marginal improvements can lead to transformative advancements, especially when it comes to algorithms and large-scale data processing.

In this journey toward optimization, one technique stands out—memoization. This article explores the significance of memoization in the context of algorithmic efficiency, and how it has become a cornerstone in the ongoing quest for computational perfection.

Table of Contents

1. Need for Optimization
2. Time Complexity
3. Recursion
4. The Problem of Redundant Computations
5. Introduction to Memoization
6. Benefits and Drawbacks
7. Real-World Examples
8. Conclusion

Need for Optimization

In computer science, optimization emerges as a fundamental and perpetual pursuit. The need for optimization becomes particularly apparent in scenarios where computations are repeated, leading to inefficiencies that impede the overall performance of algorithms.

Consider a scenario where a program executes a set of instructions, and within this set, certain computations are repeated unnecessarily. These redundancies not only consume valuable computational resources but also prolong the time it takes to accomplish a given task. In large-scale applications, such inefficiencies can escalate, resulting in sluggish performance and increased resource utilization.

Optimization, in this context, becomes a strategic approach to streamline these repetitive processes, ensuring that computations are performed with maximum efficiency. By minimizing redundancy and resource consumption, optimized algorithms contribute to faster execution times, reduced memory usage, and an overall enhancement of computational performance.

Time Complexity

To quantify and measure the efficiency of algorithms, computer scientists often rely on the concept of time complexity. Time complexity provides a theoretical framework for evaluating the runtime behavior of algorithms based on the input size. It serves as a crucial metric in determining how the algorithm's performance scales as the size of the input increases.

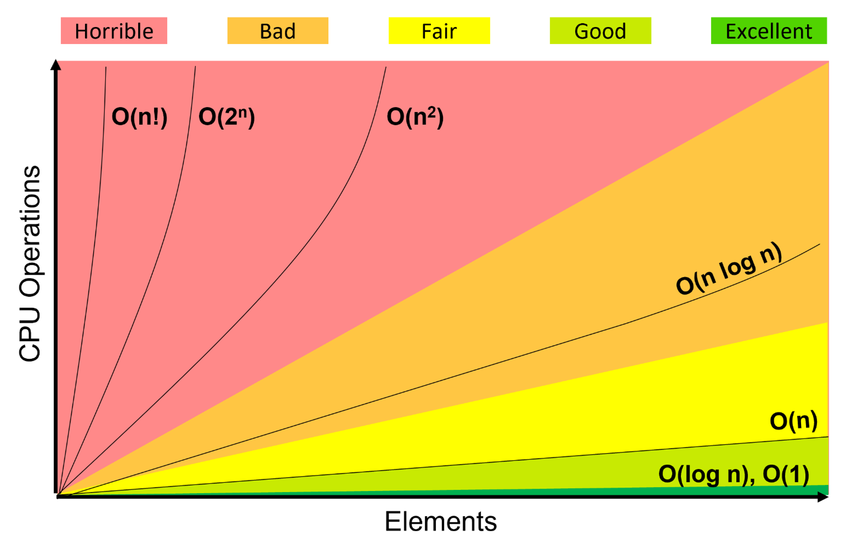Big-O time complexity chart based feature selection. (source: ResearchGate)

In simpler terms, time complexity helps answer the question: "How does the running time of an algorithm grow as the input size grows?" Algorithms with lower time complexity are generally more efficient, as they exhibit faster execution times even with larger inputs.

Understanding time complexity is essential for algorithm designers and developers aiming to create scalable and performant solutions. By analyzing and optimizing time complexity, they can design algorithms that efficiently handle a wide range of input sizes, ensuring responsiveness and reliability in various computational scenarios.

In the upcoming sections, we will explore how the technique of memoization addresses the challenges posed by repeated computations, contributing to improved time complexity and overall algorithmic efficiency.

Recursion

(source: Hemanth)

Understanding functions and recursion lays the groundwork for exploring how memoization can optimize recursive computations by avoiding redundant function calls.

Recursion is one of the main areas memoization can be used in. In simple terms, recursion is a function that calls itself. The main goal here is to divide the bigger problem into subproblems that require the same method of calculation.

Let’s see a very basic example. If you are familiar with high school maths, the factorial of a number is basically a recursive algorithm. The factorial of a non-negative integer n (denoted as n!) is the product of all positive integers up to n. In order for a very simple representation, you can see the recursive definition in Python as follows:

def factorial(n):
    # Base case
    if n == 0 or n == 1:
        return 1
    # Recursive case
    else:
        return n * factorial(n - 1)

In this example, the factorial function calls itself with a smaller argument (n - 1) until the base case is reached (n == 0 or n == 1), at which point the recursion stops. Recursion is a natural fit for certain problems and can lead to elegant and concise solutions, though it requires careful consideration of base cases to avoid infinite recursion.

The Problem of Redundant Computations

One of the inherent challenges in recursive functions is the possibility of redundancy, where the same values are computed multiple times over the execution of a function. The redundancy arises when the function is called with the same arguments more than once, leading to unnecessary computations and large overheads. In the scenarios of large datasets or complex functions, this redundancy can significantly impact the overall efficiency of the algorithm.

A very straightforward example would be the calculation of Fibonacci numbers using naive recursion (naive = no optimization). Having not optimized this algorithm, the function may recalculate Fibonacci values for the same index over and over again, leading to inefficiencies.

Let’s look at how it would look like:

def fibonacci_naive(n):
    if n <= 1:
        return n
    else:
        return fibonacci_naive(n - 1) + fibonacci_naive(n - 2)

In this naive implementation, the function recursively calculates the Fibonacci number for index n by summing the values of the two preceding indices. However, this approach results in redundant computations. For instance, when calculating fibonacci_naive(4), the function recursively computes fibonacci_naive(3) and fibonacci_naive(2). Yet, the calculation of fibonacci_naive(3) in turn redundantly recomputes fibonacci_naive(2), leading to duplicated efforts.

As the index n increases, the redundancy becomes more pronounced, and the inefficiency of recomputing the same values becomes a bottleneck in the performance of the algorithm.

Introduction to Memoization

Before diving into memoization properly we need to understand the word 'cache' first. In hardware terms, “Cache memories are used in modern, medium and high-speed CPUs to hold temporarily those portions of the contents of main memory which are (believed to be) currently in use.” Basically, when it comes to software, the idea is the same. We are temporarily storing recently used data in order to achieve better performance.

Memoization is a powerful technique that is built upon the same principle. The key idea behind it therefore, is to cache the results of expensive function calls and return the cached result when the same inputs occur again. This avoids redundant computations and dramatically improves the efficiency of algorithms.

This idea was introduced back in 1968 by a British researcher in artificial intelligence, Donald Michie, who stated:

“If computers could learn from experience their usefulness would be increased. When I write a clumsy program for a contemporary computer a thousand runs on the machine do not re-educate my handiwork. On every execution, each time-wasting blemish and crudity, each needless test and redundant evaluation, is meticulously reproduced.”

He searched for a solution to his problem and introduced 'memo' functions.

The heart of memoization lies in the memoization table, or as what you’ve already heard of — the cache. This data structure is used to store and manage the results of function calls for specific input arguments. In practice, the memoization table is often implemented as a dictionary or an array, where the input arguments serve as keys or indices, and the corresponding results are stored as values.

Let’s take that fibonacci_naive function and use the technique of memoization in order to solve it’s redundancy problem:

memo = {}

def fibonacci_memoized(n):
    if n in memo:
        return memo[n]
    if n <= 1:
        result = n
    else:
        result = fibonacci_memoized(n - 1) + fibonacci_memoized(n - 2)
    memo[n] = result
    return result

As you can see, there has been a dictionary added called memo. Before trying to call any recursive function, we check if the value we are trying to calculate with is already in our cache. If it is, we simply return that number, otherwise we go on with the computation and in the end, we store our result as the value with the key of the input. It’s. That. Simple.

The use of a memoization table transforms a recursive algorithm with redundant computations into an efficient and dynamic solution, significantly reducing time complexity and enhancing overall performance.

Now, let's compare the performance of the two versions by measuring the time taken to compute Fibonacci numbers for various indices:

import time

# [...] place for the fibonacci_naive and fibonacci_memoized functions defined earlier

# Non-memoized
start_time = time.time()
result_memoized = fibonacci_memoized(30)
end_time = time.time()
time_memoized = end_time - start_time

# Memoized
start_time = time.time()
result_naive = fibonacci_naive(30)
end_time = time.time()
time_naive = end_time - start_time

print(f"Non-Memoized Result: {result_naive}, Time: {time_naive} seconds")
print(f"Memoized Result: {result_memoized}, Time: {time_memoized} seconds")

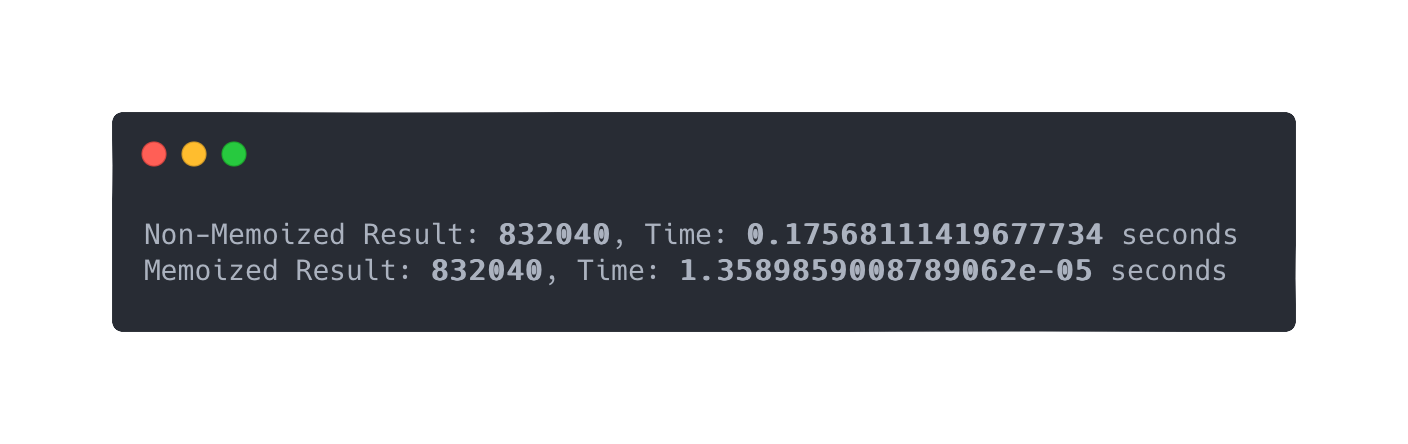
This comparison highlights the significant improvement in performance achieved by memoization. The memoized version avoids redundant computations, resulting in a faster execution time compared to the non-memoized version. As the index n increases, the performance difference becomes more pronounced.

Note: The time it took for the memoization function to calculate the result was 1.52587890625e-05 seconds. In this notation, the "e-05" at the end indicates that the decimal point is moved five places to the left, making the number smaller. So, the number is equivalent to 0.0000152587890625 in decimal form.

Benefits and Drawbacks

Memoization offers several advantages that contribute to algorithmic efficiency:

• Reduction in redundant computations
• Optimized time complexity
• Scalability, i.e., efficient handling of large inputs

On the other hand, there are some cases when memoization needs to be used with more attention:

• The memoization table can eat up a lot of space when it comes to storing large amount of data, therefore it may increase the space complexity of the algorithm. Careful consideration is needed when defining the problem the algorithm will resolve, so that the evaluation of space and time complexity can benefit the purpose of solving that particular problem.
• Memoization may pose challenges when dealing with functions that have side effects or rely on external state. Caching results assumes that the function's output is solely determined by its input parameters, which may not be true in all cases.

Real-World Examples

While completing a Flutter course on Udemy, I’ve created a 'favorite places' application, where you can take a photo of a place you like, then with the help of the Google Maps API, your current location gets stored in the application with the corresponding image. Although, what I found is that if I was at the same place, but I didn't like the photo I'd taken and wanted to take another one, the app still needed to wait for the response of the http request in order to load the data. Therefore, the good old spinning circle got shown and sometimes it can take a while, not too much, but still enough for a programmer to consider it as an opportunity for optimization. Solution? Memoization.

I simply made a key value pair storage, which in the Dart programming language is a Map, and used it as a cache. I created a PlaceLocation model class and basically each time before I was reaching out to the Google Maps API, first, I checked if the cache contained the corresponding key, which in this case was the latitude and the value was the longitude.

class PlaceLocation {
  const PlaceLocation({
    required this.latitude,
    required this.longitude,
    required this.address,
  });

  final double latitude;
  final double longitude;
  final String address;
}

// A riverpod provider class to store the cached values
class PlaceLocationCacheNotifier
    extends StateNotifier<Map<String, PlaceLocation>> {
  PlaceLocationCacheNotifier() : super({});

  void cache(String key, PlaceLocation location) {
    state = {...state, key: location};
  }
}

final placeLocationCacheProvider = StateNotifierProvider<
    PlaceLocationCacheNotifier,
    Map<String, PlaceLocation>>((ref) => PlaceLocationCacheNotifier());

//...
// Using the logic of memoization
if (locationCache.containsKey('$lat,$lng')) {
      setState(() {
        _pickedLocation = locationCache['$lat,$lng'];
        _isGettingLocation = false;
      });
    } else {
      final key = FlutterConfig.get('GOOGLE_MAPS_API_KEY');

      final url = Uri.parse(
          'https://maps.googleapis.com/maps/api/geocode/json?latlng=$lat,$lng&key=$key');

      final response = await http.get(url);
      final resData = json.decode(response.body);

      final address = resData['results'][0]['formatted_address'];

      setState(() {
        _pickedLocation = PlaceLocation(
          latitude: lat,
          longitude: lng,
          address: address,
        );
        _isGettingLocation = false;
      });
      ref
          .watch(placeLocationCacheProvider.notifier)
          .cache('$lat,$lng', _pickedLocation!);
    }

If you’d like to check out the full application, you can find it on my Github profile.

Other than this data fetching usecase, memoization can also be used in:

• The aforementioned Fibonacci sequence calculations
• Longest Common Subsequence (LCS)
• Knapsack Problem
• Binary tree algorithms
• Pathfinding algorithms
• Sequence Alignment Algorithms

and of course the list could go on.

Conclusion

In conclusion, memoization stands as a crucial optimization technique, addressing the challenge of redundant computations in algorithms. Memoization's ability to significantly enhance algorithmic efficiency, reduce time complexity, and provide versatility across various domains—from dynamic programming problems to real-world applications in AI, game development, and beyond—has been demonstrated. Memoization is a key tool for developers, offering improved performance, optimized time complexity, and the simplicity of cleaner, more readable code.